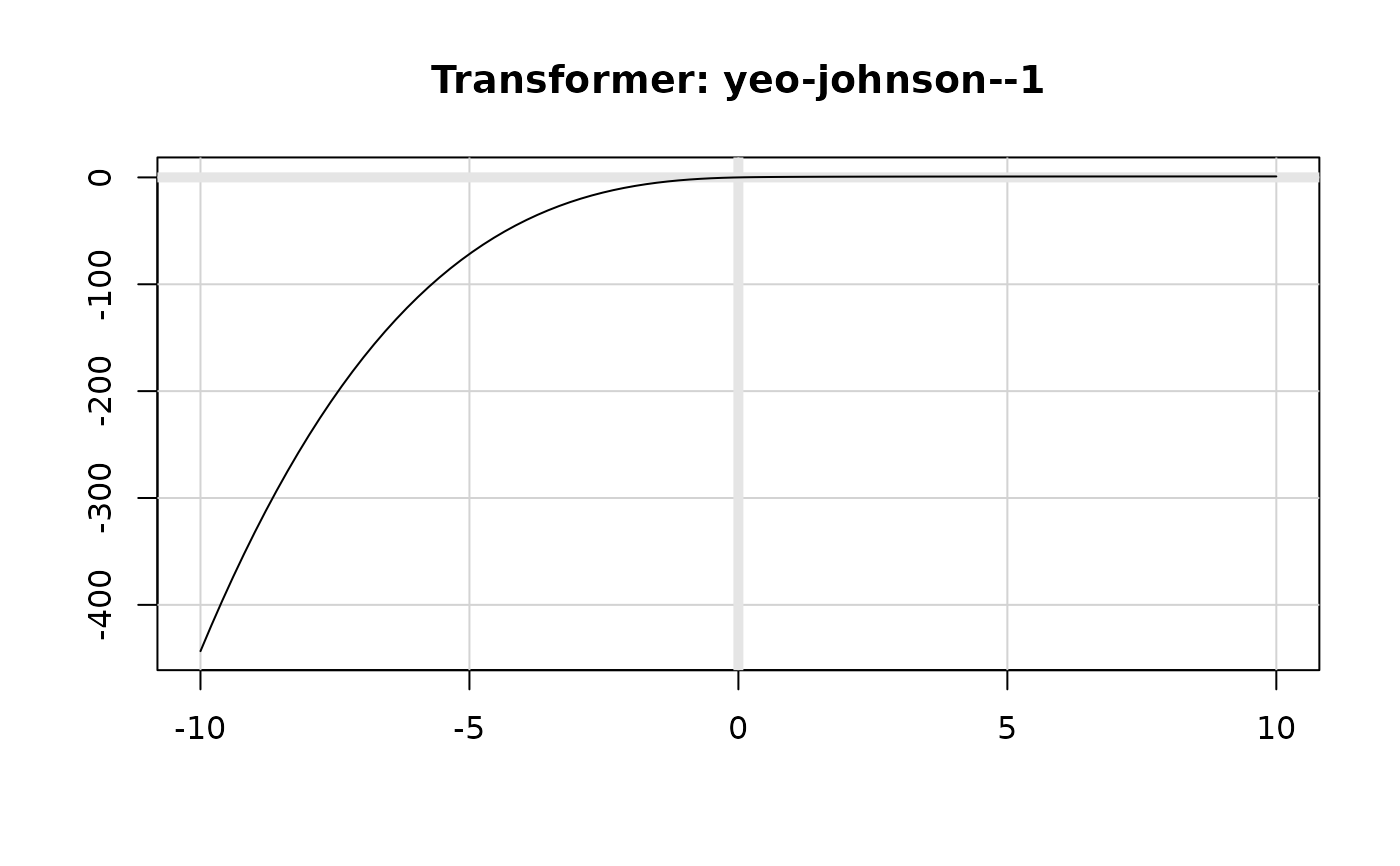
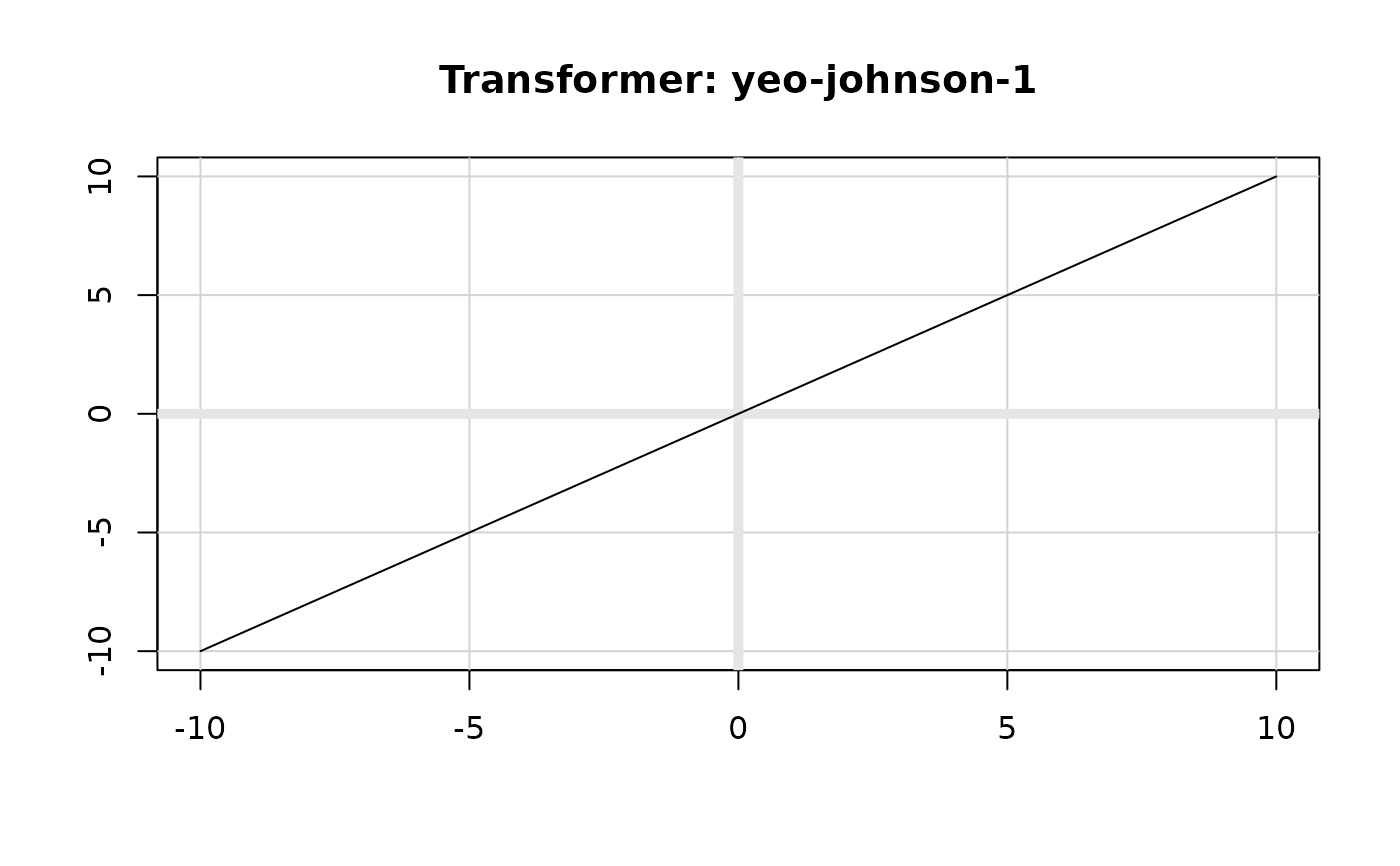
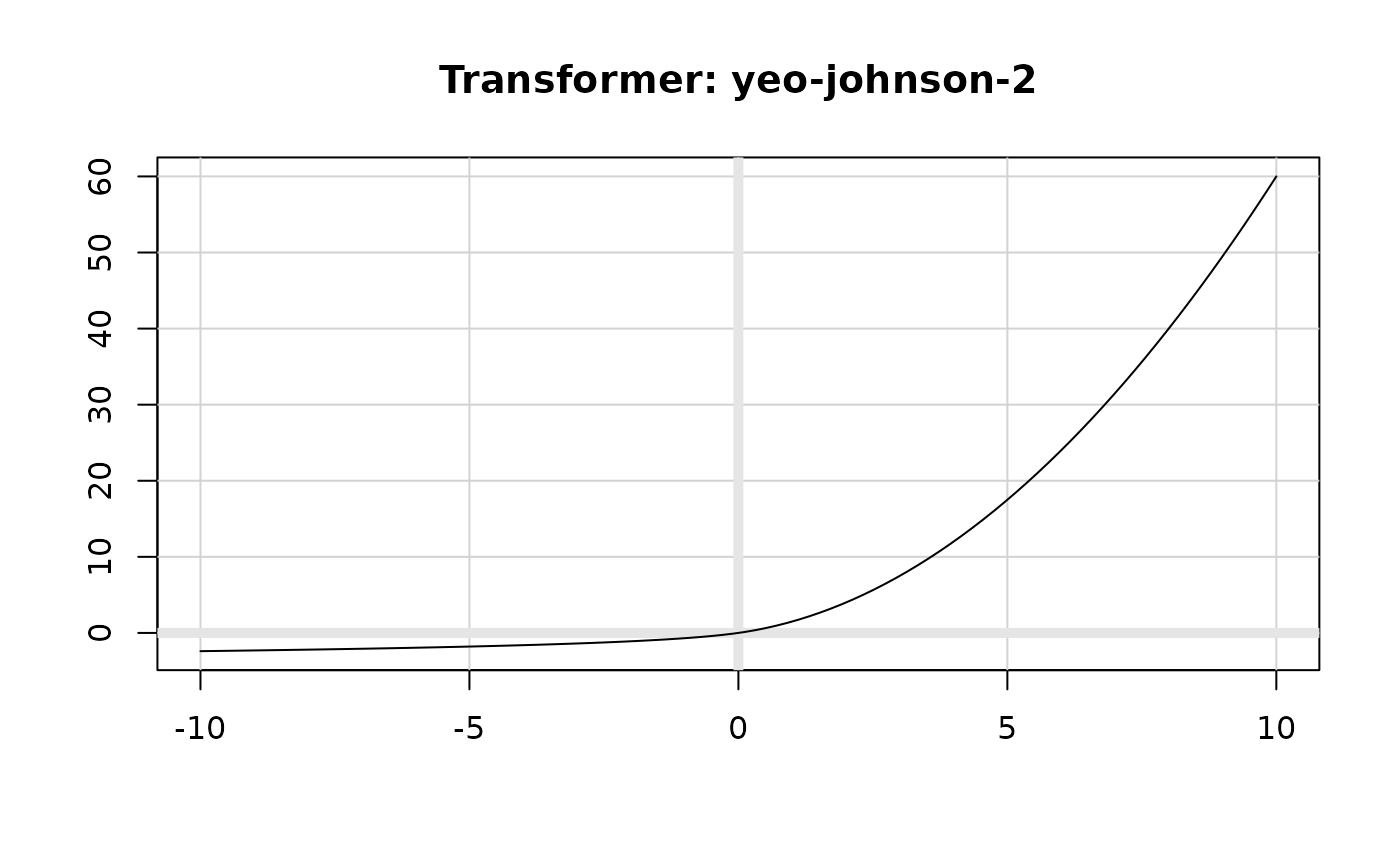
Yeo-Johnson transformation — transform

The Yeo-Johnson transformation is a flexible transformation that is similar to Box-Cox, transform_boxcox(), but does not require input values to be greater than zero.

Usage

transform_yj(p)

yj_trans(p)

Arguments

p: Transformation exponent, \(\lambda\).

Details

The transformation takes one of four forms depending on the values of y and \(\lambda\).

\(y \ge 0\) and \(\lambda \neq 0\) : \(y^{(\lambda)} = \frac{(y + 1)^\lambda - 1}{\lambda}\)
\(y \ge 0\) and \(\lambda = 0\): \(y^{(\lambda)} = \ln(y + 1)\)
\(y < 0\) and \(\lambda \neq 2\): \(y^{(\lambda)} = -\frac{(-y + 1)^{(2 - \lambda)} - 1}{2 - \lambda}\)
\(y < 0\) and \(\lambda = 2\): \(y^{(\lambda)} = -\ln(-y + 1)\)

References

Yeo, I., & Johnson, R. (2000). A New Family of Power Transformations to Improve Normality or Symmetry. Biometrika, 87(4), 954-959. https://www.jstor.org/stable/2673623

Examples

plot(transform_yj(-1), xlim = c(-10, 10))

plot(transform_yj(0), xlim = c(-10, 10))

plot(transform_yj(1), xlim = c(-10, 10))

plot(transform_yj(2), xlim = c(-10, 10))