The Box-Cox transformation is a flexible transformation, often used to transform data towards normality. The modulus transformation generalises Box-Cox to also work with negative values.
Usage
transform_boxcox(p, offset = 0)
boxcox_trans(p, offset = 0)
transform_modulus(p, offset = 1)
modulus_trans(p, offset = 1)Details
The Box-Cox power transformation (type 1) requires strictly positive values and takes the following form for \(\lambda > 0\): $$y^{(\lambda)} = \frac{y^\lambda - 1}{\lambda}$$ When \(\lambda = 0\), the natural log transform is used.
The modulus transformation implements a generalisation of the Box-Cox transformation that works for data with both positive and negative values. The equation takes the following forms, when \(\lambda \neq 0\) : $$y^{(\lambda)} = sign(y) * \frac{(|y| + 1)^\lambda - 1}{\lambda}$$ and when \(\lambda = 0\): $$y^{(\lambda)} = sign(y) * \ln(|y| + 1)$$
References
Box, G. E., & Cox, D. R. (1964). An analysis of transformations. Journal of the Royal Statistical Society. Series B (Methodological), 211-252. https://www.jstor.org/stable/2984418
John, J. A., & Draper, N. R. (1980). An alternative family of transformations. Applied Statistics, 190-197. https://www.jstor.org/stable/2986305
Examples
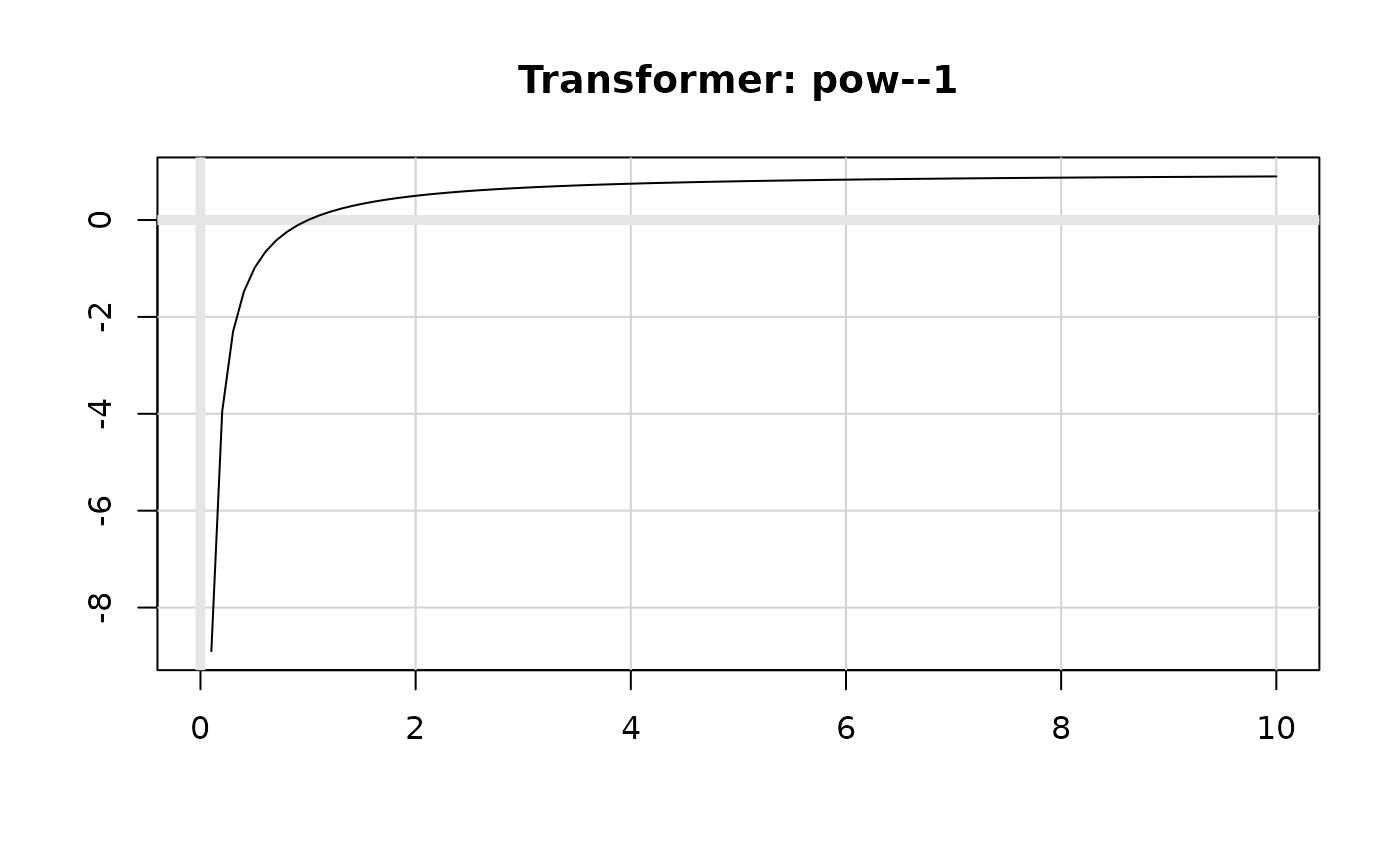
plot(transform_boxcox(-1), xlim = c(0, 10))
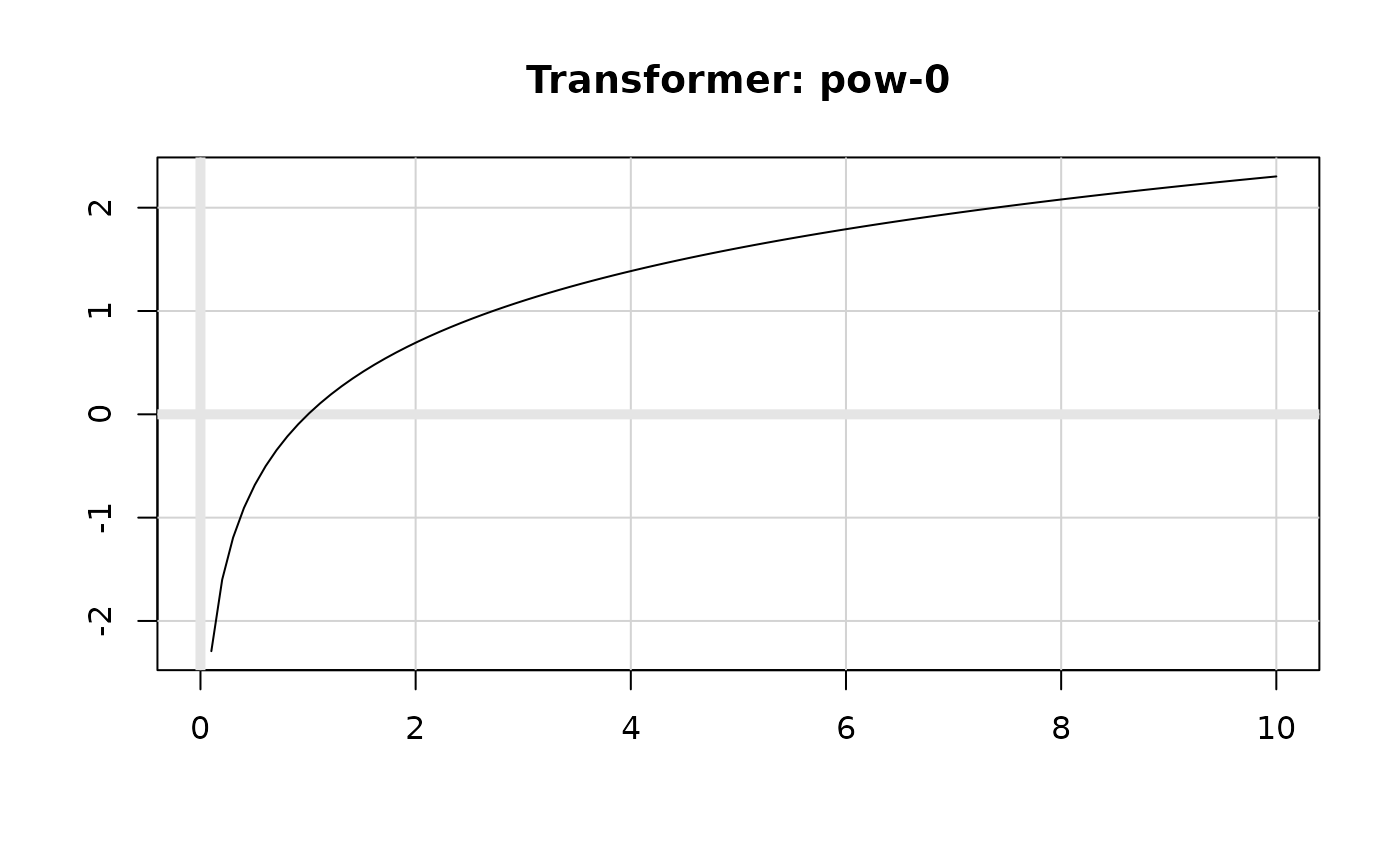
 plot(transform_boxcox(0), xlim = c(0, 10))
plot(transform_boxcox(0), xlim = c(0, 10))
 plot(transform_boxcox(1), xlim = c(0, 10))
plot(transform_boxcox(1), xlim = c(0, 10))
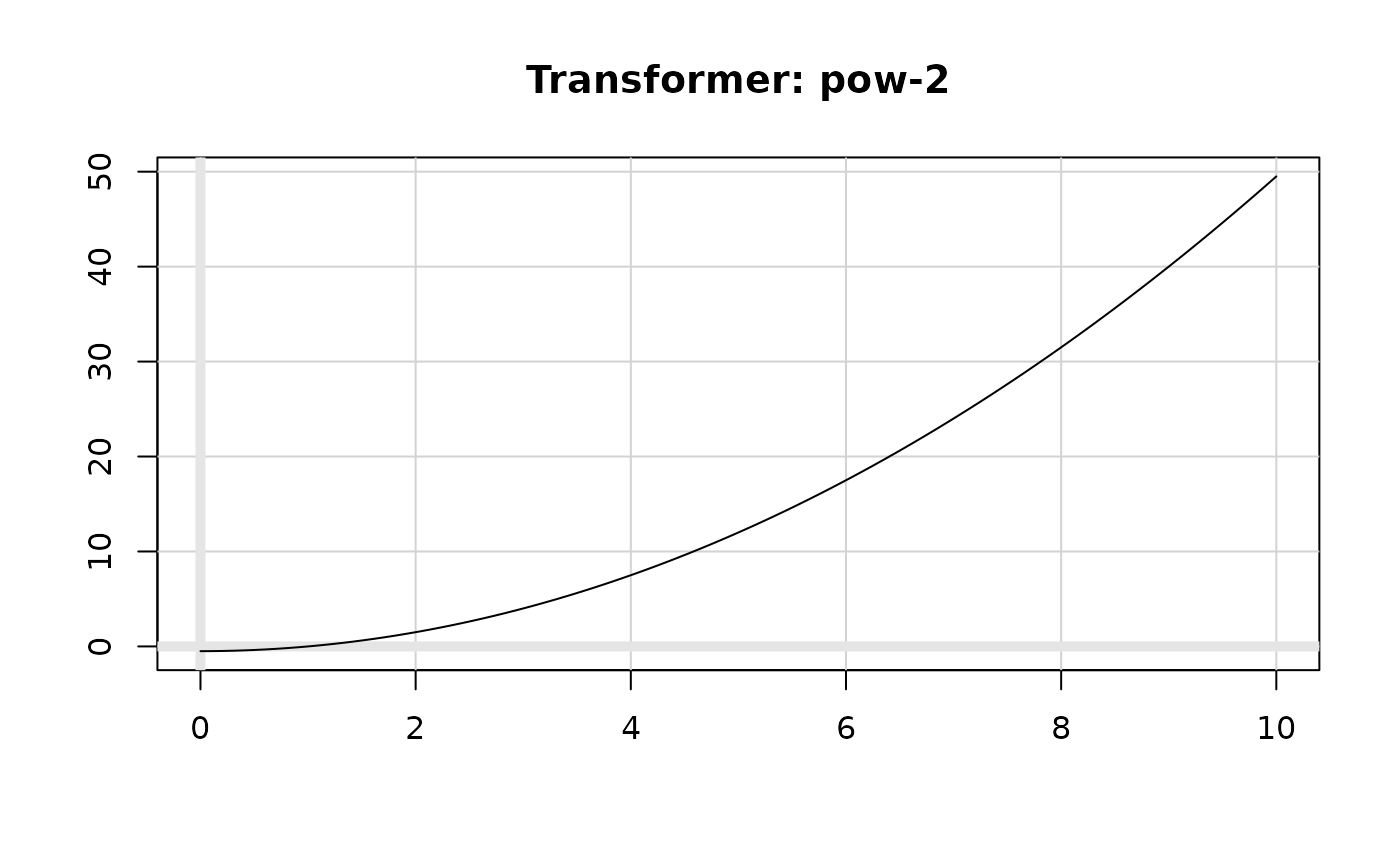
 plot(transform_boxcox(2), xlim = c(0, 10))
plot(transform_boxcox(2), xlim = c(0, 10))
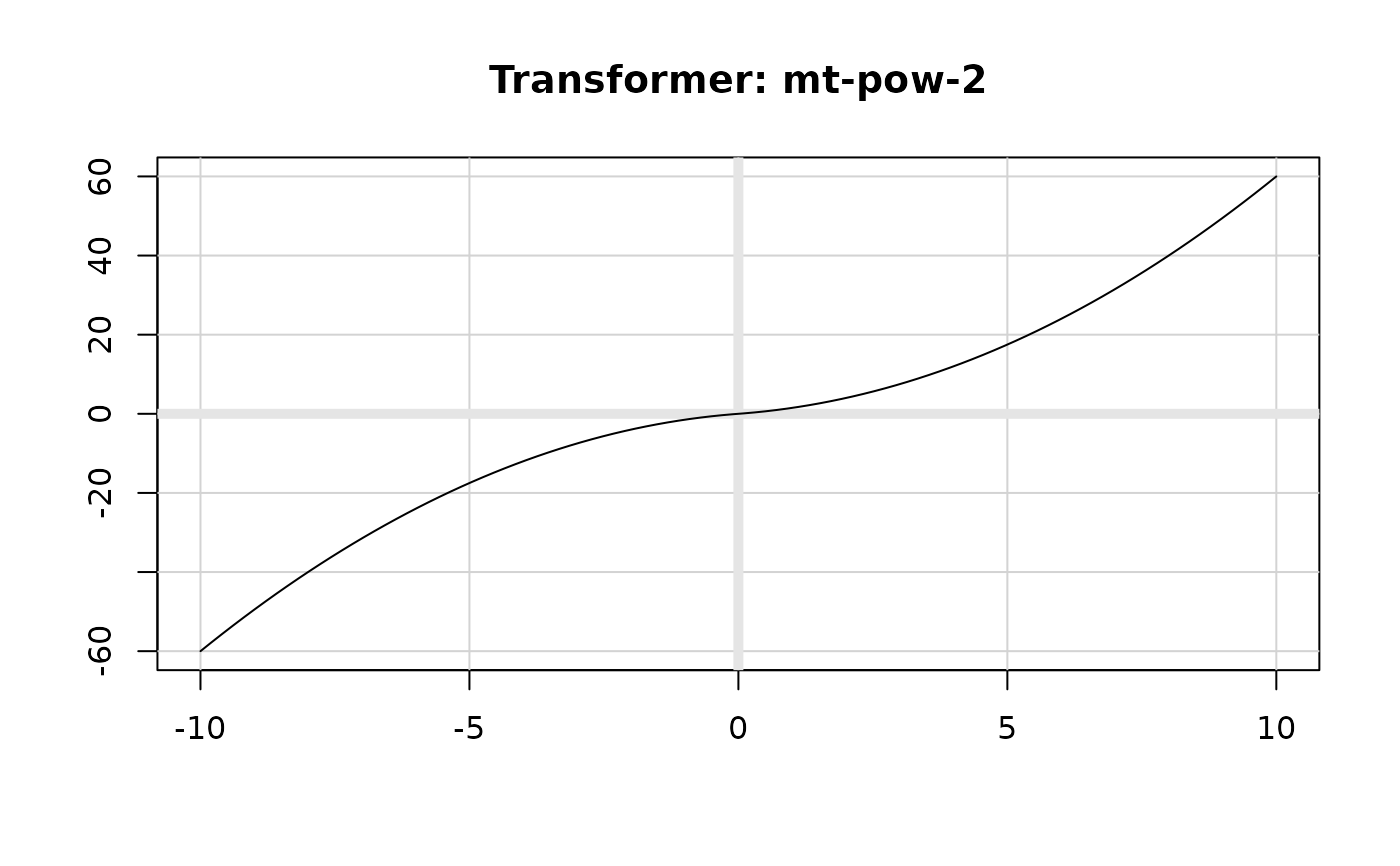
 plot(transform_modulus(-1), xlim = c(-10, 10))
plot(transform_modulus(-1), xlim = c(-10, 10))
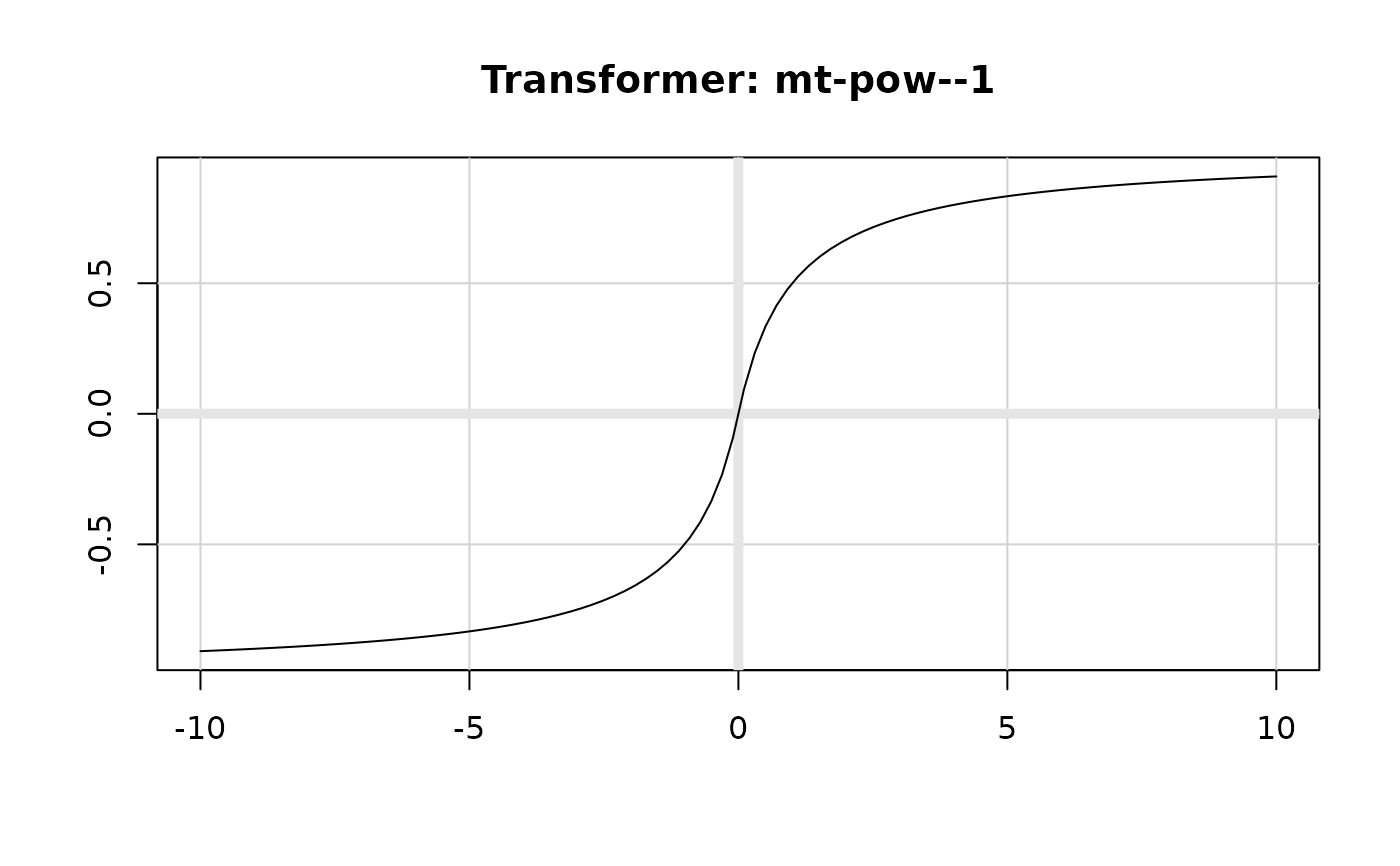 plot(transform_modulus(0), xlim = c(-10, 10))
plot(transform_modulus(0), xlim = c(-10, 10))
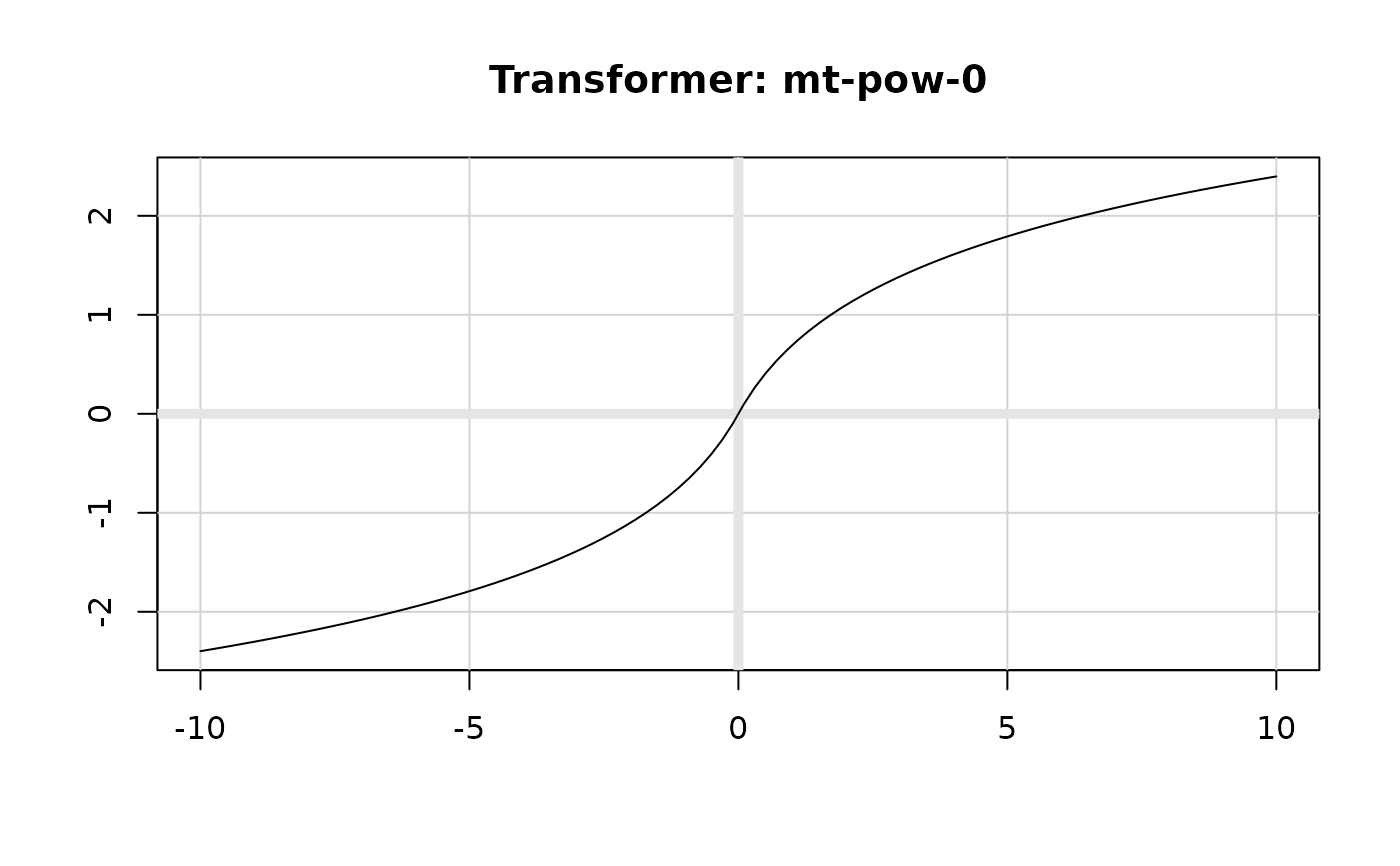 plot(transform_modulus(1), xlim = c(-10, 10))
plot(transform_modulus(1), xlim = c(-10, 10))
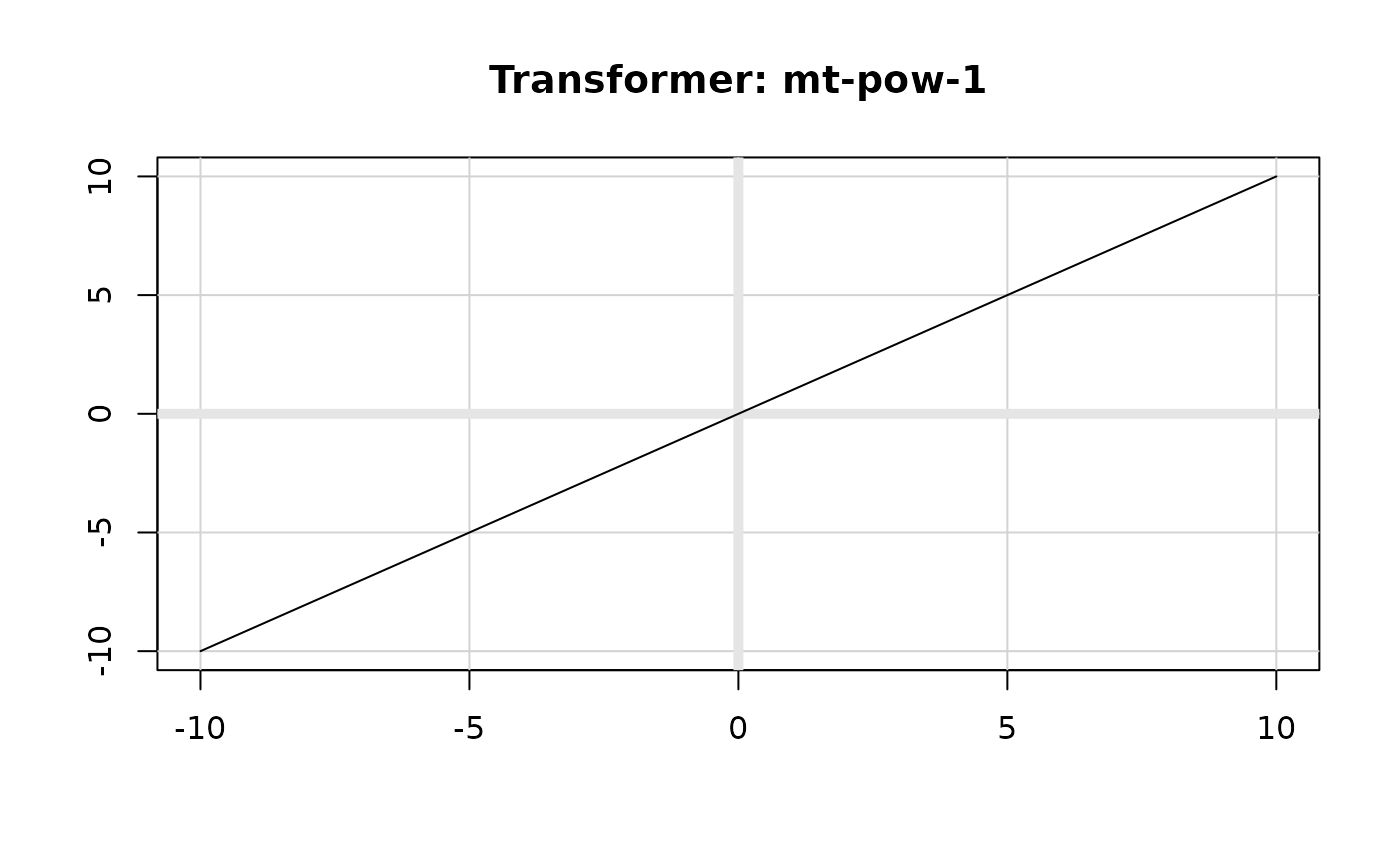 plot(transform_modulus(2), xlim = c(-10, 10))
plot(transform_modulus(2), xlim = c(-10, 10))